Cosine Sum And Difference Identities

Learning Objectives

In this department, you will:

• Use sum and difference formulas for cosine.
• Use sum and divergence formulas for sine.
• Use sum and difference formulas for tangent.
• Apply sum and difference formulas for cofunctions.
• Use sum and difference formulas to verify identities.

Figure 1. Mountain McKinley, in Denali National Park, Alaska, rises 20,237 anxiety (6,168 m) above body of water level. It is the highest superlative in North America. (credit: Daniel A. Leifheit, Flickr)

How tin can the height of a mountain be measured? What about the distance from Earth to the sun? Similar many seemingly incommunicable problems, nosotros rely on mathematical formulas to find the answers. The trigonometric identities, commonly used in mathematical proofs, have had real-world applications for centuries, including their employ in calculating long distances.

The trigonometric identities we volition examine in this section can exist traced to a Farsi astronomer who lived around 950 Ad, but the ancient Greeks discovered these aforementioned formulas much before and stated them in terms of chords. These are special equations or postulates, true for all values input to the equations, and with innumerable applications.

In this section, we will learn techniques that will enable us to solve problems such every bit the ones presented higher up. The formulas that follow will simplify many trigonometric expressions and equations. Keep in heed that, throughout this section, the term formula is used synonymously with the word identity.

Using the Sum and Difference Formulas for Cosine

Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite the given angle in terms of two angles that take known trigonometric values. Nosotros can apply the special angles, which we tin can review in the unit of measurement circle shown in (Figure).

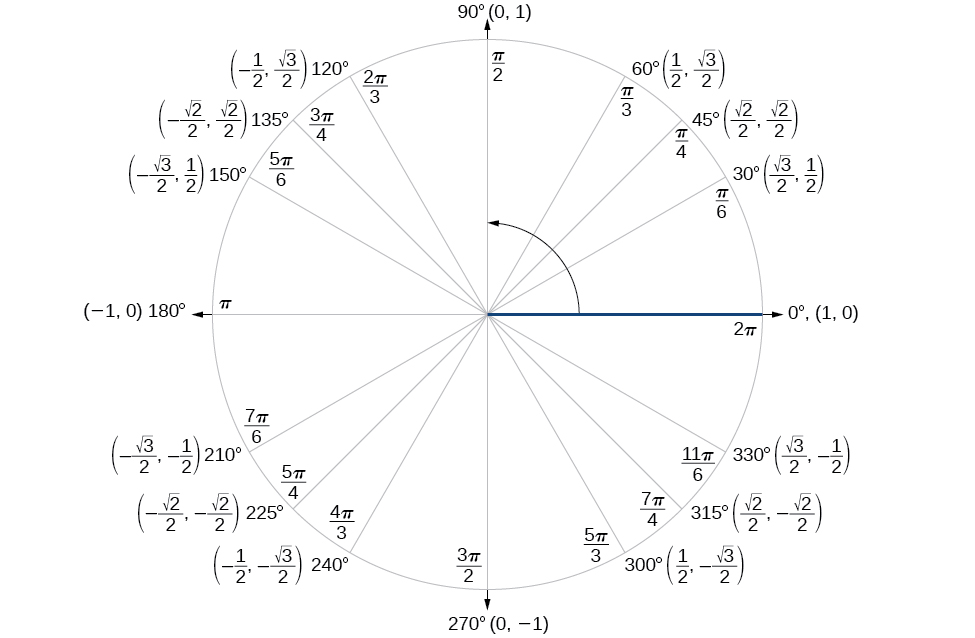
Figure 2. The Unit of measurement Circle

We will begin with the sum and deviation formulas for cosine, then that we can find the cosine of a given angle if nosotros tin break it upward into the sum or difference of ii of the special angles. Run across (Figure).

Sum formula for cosine	[latex]\mathrm{cos}\left(\alpha +\beta \correct)=\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta [/latex]
Divergence formula for cosine	[latex]\mathrm{cos}\left(\alpha -\beta \right)=\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta +\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta [/latex]

First, we volition evidence the difference formula for cosines. Let'due south consider 2 points on the unit circle. Come across (Effigy). Point[latex]\,P\,[/latex]is at an angle[latex]\,\alpha \,[/latex]from the positive x-centrality with coordinates[latex]\,\left(\mathrm{cos}\,\alpha ,\mathrm{sin}\,\alpha \right)\,[/latex]and bespeak[latex]\,Q\,[/latex]is at an angle of[latex]\,\beta \,[/latex]from the positive x-axis with coordinates[latex]\,\left(\mathrm{cos}\,\beta ,\mathrm{sin}\,\beta \correct).\,[/latex]Note the measure out of angle[latex]\,POQ\,[/latex]is[latex]\,\alpha -\beta .\,[/latex]

Label two more points:[latex]\,A\,[/latex]at an bending of[latex]\,\left(\alpha -\beta \right)\,[/latex]from the positive ten-axis with coordinates[latex]\,\left(\mathrm{cos}\left(\alpha -\beta \right),\mathrm{sin}\left(\blastoff -\beta \correct)\correct);\,[/latex]and point[latex]\,B\,[/latex]with coordinates[latex]\,\left(1,0\right).\,[/latex]Triangle[latex]\,POQ\,[/latex]is a rotation of triangle[latex]\,AOB\,[/latex]and thus the distance from[latex]\,P\,[/latex]to[latex]\,Q\,[/latex]is the same every bit the altitude from[latex]\,A\,[/latex]to[latex]\,B.[/latex]

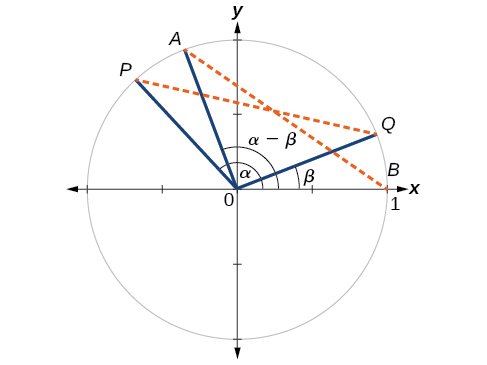
Effigy 3.

We can find the distance from[latex]\,P\,[/latex]to[latex]\,Q\,[/latex]using the distance formula.

[latex]\begin{assortment}{ccc}\hfill {d}_{PQ}& =& \sqrt{{\left(\mathrm{cos}\,\alpha -\mathrm{cos}\,\beta \right)}^{two}+{\left(\mathrm{sin}\,\alpha -\mathrm{sin}\,\beta \right)}^{2}}\hfill \\ & =& \sqrt{{\mathrm{cos}}^{2}\alpha -ii\,\mathrm{cos}\,\blastoff \,\mathrm{cos}\,\beta +{\mathrm{cos}}^{2}\beta +{\mathrm{sin}}^{2}\alpha -ii\,\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta +{\mathrm{sin}}^{2}\beta }\hfill \end{array}[/latex]

And so we apply the Pythagorean identity and simplify.

[latex]\begin{array}{cc}=& \sqrt{\left({\mathrm{cos}}^{ii}\alpha +{\mathrm{sin}}^{ii}\alpha \right)+\left({\mathrm{cos}}^{2}\beta +{\mathrm{sin}}^{2}\beta \right)-2\,\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -two\,\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta }\hfill \\ =& \sqrt{i+1-two\,\mathrm{cos}\,\blastoff \,\mathrm{cos}\,\beta -2\,\mathrm{sin}\,\blastoff \,\mathrm{sin}\,\beta }\hfill \\ =& \sqrt{two-2\,\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -2\,\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta }\hfill \end{array}[/latex]

Similarly, using the altitude formula we can discover the distance from[latex]\,A\,[/latex]to[latex]\,B.[/latex]

[latex]\begin{array}{ccc}\hfill {d}_{AB}& =& \sqrt{{\left(\mathrm{cos}\left(\alpha -\beta \right)-i\right)}^{2}+{\left(\mathrm{sin}\left(\blastoff -\beta \correct)-0\right)}^{2}}\hfill \\ & =& \sqrt{{\mathrm{cos}}^{2}\left(\alpha -\beta \right)-2\,\mathrm{cos}\left(\alpha -\beta \right)+ane+{\mathrm{sin}}^{2}\left(\alpha -\beta \right)}\hfill \finish{array}[/latex]

Applying the Pythagorean identity and simplifying nosotros get:

[latex]\begin{array}{cc}=& \sqrt{\left({\mathrm{cos}}^{2}\left(\alpha -\beta \right)+{\mathrm{sin}}^{2}\left(\alpha -\beta \right)\right)-two\,\mathrm{cos}\left(\blastoff -\beta \right)+1}\hfill \\ =& \sqrt{1-2\,\mathrm{cos}\left(\alpha -\beta \right)+1}\hfill \\ =& \sqrt{2-ii\,\mathrm{cos}\left(\alpha -\beta \right)}\hfill \end{array}[/latex]

Because the two distances are the same, we gear up them equal to each other and simplify.

[latex]\brainstorm{array}{ccc}\hfill \sqrt{2-two\,\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -2\,\mathrm{sin}\,\blastoff \,\mathrm{sin}\,\beta }& =& \sqrt{2-2\,\mathrm{cos}\left(\alpha -\beta \right)}\hfill \\ \hfill ii-two\,\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -2\,\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta & =& 2-ii\,\mathrm{cos}\left(\alpha -\beta \right)\hfill \stop{array}[/latex]

Finally we subtract[latex]\,ii\,[/latex]from both sides and divide both sides past[latex]\,-ii.[/latex]

[latex]\mathrm{cos}\,\blastoff \,\mathrm{cos}\,\beta +\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta =\mathrm{cos}\left(\alpha -\beta \right)\text{ }[/latex]

Thus, nosotros have the difference formula for cosine. We tin can use similar methods to derive the cosine of the sum of two angles.

Sum and Difference Formulas for Cosine

These formulas tin can be used to calculate the cosine of sums and differences of angles.

[latex]\mathrm{cos}\left(\alpha +\beta \right)=\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -\mathrm{sin}\,\blastoff \,\mathrm{sin}\,\beta [/latex]

[latex]\mathrm{cos}\left(\alpha -\beta \correct)=\mathrm{cos}\,\blastoff \,\mathrm{cos}\,\beta +\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta [/latex]

How To

Given two angles, find the cosine of the difference between the angles.

1. Write the departure formula for cosine.
2. Substitute the values of the given angles into the formula.
3. Simplify.

Finding the Exact Value Using the Formula for the Cosine of the Difference of Two Angles

Using the formula for the cosine of the difference of two angles, find the exact value of[latex]\,\mathrm{cos}\left(\frac{5\pi }{4}-\frac{\pi }{6}\right).[/latex]

Effort It

Find the exact value of[latex]\,\mathrm{cos}\left(\frac{\pi }{3}-\frac{\pi }{iv}\right).[/latex]

Show Solution

[latex]\frac{\sqrt{ii}+\sqrt{half-dozen}}{4}[/latex]

Finding the Exact Value Using the Formula for the Sum of Two Angles for Cosine

Find the exact value of[latex]\,\mathrm{cos}\left(75°\correct).[/latex]

Analysis

Notation that we could take also solved this trouble using the fact that[latex]\,75°=135°-sixty°.[/latex]

[latex]\begin{array}{ccc}\hfill \mathrm{cos}\left(\alpha -\beta \correct)& =& \mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta +\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta \hfill \\ \hfill \mathrm{cos}\left(135°-threescore°\right)& =& \mathrm{cos}\left(135°\right)\mathrm{cos}\left(60°\right)+\mathrm{sin}\left(135°\right)\mathrm{sin}\left(60°\right)\hfill \\ & =& \left(-\frac{\sqrt{2}}{2}\correct)\left(\frac{i}{2}\correct)+\left(\frac{\sqrt{2}}{2}\right)\left(\frac{\sqrt{three}}{2}\right)\hfill \\ & =& \left(-\frac{\sqrt{2}}{4}\right)+\left(\frac{\sqrt{6}}{4}\right)\hfill \\ & =& \left(\frac{\sqrt{6}-\sqrt{2}}{4}\correct)\hfill \stop{assortment}[/latex]

Attempt It

Find the exact value of[latex]\,\mathrm{cos}\left(105°\correct).[/latex]

Show Solution

[latex]\frac{\sqrt{2}-\sqrt{half-dozen}}{4}[/latex]

Using the Sum and Difference Formulas for Sine

The sum and divergence formulas for sine tin exist derived in the same manner as those for cosine, and they resemble the cosine formulas.

Sum and Departure Formulas for Sine

These formulas can exist used to calculate the sines of sums and differences of angles.

[latex]\mathrm{sin}\left(\alpha +\beta \right)=\mathrm{sin}\,\alpha \,\mathrm{cos}\,\beta +\mathrm{cos}\,\alpha \,\mathrm{sin}\,\beta [/latex]

[latex]\mathrm{sin}\left(\alpha -\beta \right)=\mathrm{sin}\,\blastoff \,\mathrm{cos}\,\beta -\mathrm{cos}\,\alpha \,\mathrm{sin}\,\beta [/latex]

How To

Given two angles, find the sine of the difference between the angles.

1. Write the divergence formula for sine.
2. Substitute the given angles into the formula.
3. Simplify.

Using Sum and Difference Identities to Evaluate the Divergence of Angles

Utilize the sum and departure identities to evaluate the difference of the angles and prove that function a equals part b.

1. [latex]\mathrm{sin}\left(45°-30°\right)[/latex]
2. [latex]\mathrm{sin}\left(135°-120°\right)[/latex]

Finding the Exact Value of an Expression Involving an Inverse Trigonometric Office

Find the exact value of[latex]\,\mathrm{sin}\left({\mathrm{cos}}^{-ane}\frac{one}{2}+{\mathrm{sin}}^{-one}\frac{3}{5}\right).\,[/latex]Then check the answer with a graphing figurer.

Using the Sum and Difference Formulas for Tangent

Finding exact values for the tangent of the sum or divergence of two angles is a little more complicated, only again, it is a matter of recognizing the pattern.

Finding the sum of 2 angles formula for tangent involves taking caliber of the sum formulas for sine and cosine and simplifying. Recall,[latex]\,\mathrm{tan}\,x=\frac{\mathrm{sin}\,x}{\mathrm{cos}\,x},\mathrm{cos}\,x\ne 0.[/latex]

Allow'southward derive the sum formula for tangent.

[latex]\begin{array}{cccc}\hfill \mathrm{tan}\left(\alpha +\beta \right)& =& \frac{\mathrm{sin}\left(\alpha +\beta \right)}{\mathrm{cos}\left(\alpha +\beta \right)}\hfill & \\ & =& \frac{\mathrm{sin}\,\blastoff \,\mathrm{cos}\,\beta +\mathrm{cos}\,\alpha \,\mathrm{sin}\,\beta }{\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta }\hfill & \\ & =& \frac{\frac{\mathrm{sin}\,\alpha \,\mathrm{cos}\,\beta +\mathrm{cos}\,\alpha \,\mathrm{sin}\,\beta }{\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta }}{\frac{\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta -\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta }{\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta }}\hfill & \text{Carve up the numerator and denominator past cos}\,\alpha \,\text{cos}\,\beta .\hfill \\ & =& \frac{\frac{\mathrm{sin}\,\alpha \overline{)\,\mathrm{cos}\,\beta }}{\mathrm{cos}\,\alpha \overline{)\,\mathrm{cos}\,\beta }}+\frac{\overline{)\mathrm{cos}\,\alpha }\,\mathrm{sin}\,\beta }{\overline{)\mathrm{cos}\,\alpha }\,\mathrm{cos}\,\beta }}{\frac{\overline{)\mathrm{cos}\,\alpha }\overline{)\,\mathrm{cos}\,\beta }}{\overline{)\mathrm{cos}\,\blastoff }\,\overline{)\mathrm{cos}\,\beta }}-\frac{\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta }{\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta }}\hfill & \\ & =& \frac{\frac{\mathrm{sin}\,\blastoff }{\mathrm{cos}\,\blastoff }+\frac{\mathrm{sin}\,\beta }{\mathrm{cos}\,\beta }}{1-\frac{\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta }{\mathrm{cos}\,\blastoff \,\mathrm{cos}\,\beta }}\hfill & \\ & =& \frac{\mathrm{tan}\,\alpha +\mathrm{tan}\,\beta }{1-\mathrm{tan}\,\alpha \,\mathrm{tan}\,\beta }\hfill & \end{array}[/latex]

We can derive the divergence formula for tangent in a similar way.

Sum and Difference Formulas for Tangent

The sum and difference formulas for tangent are:

[latex]\mathrm{tan}\left(\alpha +\beta \right)=\frac{\mathrm{tan}\,\blastoff +\mathrm{tan}\,\beta }{ane-\mathrm{tan}\,\alpha \,\mathrm{tan}\,\beta }[/latex]

[latex]\mathrm{tan}\left(\blastoff -\beta \correct)=\frac{\mathrm{tan}\,\alpha -\mathrm{tan}\,\beta }{1+\mathrm{tan}\,\blastoff \,\mathrm{tan}\,\beta }[/latex]

How To

Given 2 angles, observe the tangent of the sum of the angles.

1. Write the sum formula for tangent.
2. Substitute the given angles into the formula.
3. Simplify.

Finding the Exact Value of an Expression Involving Tangent

Discover the exact value of[latex]\,\mathrm{tan}\left(\frac{\pi }{6}+\frac{\pi }{4}\right).[/latex]

Try It

Find the exact value of[latex]\,\mathrm{tan}\left(\frac{two\pi }{3}+\frac{\pi }{iv}\correct).[/latex]

Show Solution

[latex]\frac{1-\sqrt{3}}{ane+\sqrt{3}}[/latex]

Finding Multiple Sums and Differences of Angles

Given[latex]\text{ }\mathrm{sin}\,\alpha =\frac{3}{v},0<\alpha <\frac{\pi }{2},\mathrm{cos}\,\beta =-\frac{five}{13},\pi <\beta <\frac{3\pi }{2},[/latex]notice

1. [latex]\mathrm{sin}\left(\blastoff +\beta \right)[/latex]
2. [latex]\mathrm{cos}\left(\blastoff +\beta \right)[/latex]
3. [latex]\mathrm{tan}\left(\blastoff +\beta \correct)[/latex]
4. [latex]\mathrm{tan}\left(\alpha -\beta \right)[/latex]

Assay

A common mistake when addressing problems such as this one is that we may be tempted to recall that[latex]\,\alpha \,[/latex]and[latex]\,\beta \,[/latex]are angles in the same triangle, which of course, they are not. Likewise note that

[latex]\mathrm{tan}\left(\alpha +\beta \right)=\frac{\mathrm{sin}\left(\blastoff +\beta \right)}{\mathrm{cos}\left(\blastoff +\beta \right)}[/latex]

Using Sum and Divergence Formulas for Cofunctions

Now that we tin can find the sine, cosine, and tangent functions for the sums and differences of angles, we can use them to do the same for their cofunctions. Y'all may remember from Right Triangle Trigonometry that, if the sum of two positive angles is[latex]\,\frac{\pi }{two},[/latex]those two angles are complements, and the sum of the two acute angles in a right triangle is[latex]\,\frac{\pi }{2},[/latex]so they are also complements. In (Figure), notice that if 1 of the acute angles is labeled as[latex]\,\theta ,[/latex]then the other acute bending must be labeled[latex]\,\left(\frac{\pi }{2}-\theta \correct).[/latex]

Notice too that[latex]\,\mathrm{sin}\,\theta =\mathrm{cos}\left(\frac{\pi }{2}-\theta \correct),[/latex]which is opposite over hypotenuse. Thus, when ii angles are complementary, we can say that the sine of[latex]\,\theta \,[/latex]equals the cofunction of the complement of[latex]\,\theta .\,[/latex]Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.

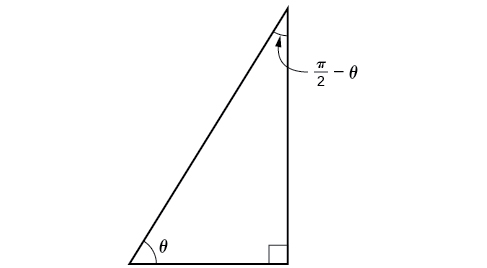
Figure 6.

From these relationships, the cofunction identities are formed. Recall that y'all first encountered these identities in The Unit Circle: Sine and Cosine Functions.

Cofunction Identities

The cofunction identities are summarized in (Figure).

[latex]\mathrm{sin}\,\theta =\mathrm{cos}\left(\frac{\pi }{2}-\theta \right)[/latex]	[latex]\mathrm{cos}\,\theta =\mathrm{sin}\left(\frac{\pi }{ii}-\theta \correct)[/latex]
[latex]\mathrm{tan}\,\theta =\mathrm{cot}\left(\frac{\pi }{2}-\theta \right)[/latex]	[latex]\mathrm{cot}\,\theta =\mathrm{tan}\left(\frac{\pi }{2}-\theta \correct)[/latex]
[latex]\mathrm{sec}\,\theta =\mathrm{csc}\left(\frac{\pi }{2}-\theta \right)[/latex]	[latex]\mathrm{csc}\,\theta =\mathrm{sec}\left(\frac{\pi }{ii}-\theta \right)[/latex]

Notice that the formulas in the tabular array may also justified algebraically using the sum and deviation formulas. For example, using

[latex]\mathrm{cos}\left(\alpha -\beta \correct)=\mathrm{cos}\,\blastoff \mathrm{cos}\,\beta +\mathrm{sin}\,\alpha \mathrm{sin}\,\beta ,[/latex]

we can write

[latex]\begin{assortment}{ccc}\hfill \mathrm{cos}\left(\frac{\pi }{2}-\theta \correct)& =& \mathrm{cos}\,\frac{\pi }{ii}\,\mathrm{cos}\,\theta +\mathrm{sin}\,\frac{\pi }{2}\,\mathrm{sin}\,\theta \hfill \\ & =& \left(0\correct)\mathrm{cos}\,\theta +\left(1\right)\mathrm{sin}\,\theta \hfill \\ & =& \mathrm{sin}\,\theta \hfill \end{array}[/latex]

Finding a Cofunction with the Same Value as the Given Expression

Write[latex]\,\mathrm{tan}\,\frac{\pi }{nine}\,[/latex]in terms of its cofunction.

Try It

Write[latex]\,\mathrm{sin}\,\frac{\pi }{vii}\,[/latex]in terms of its cofunction.

Show Solution

[latex]\mathrm{cos}\left(\frac{5\pi }{14}\correct)[/latex]

Using the Sum and Deviation Formulas to Verify Identities

Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them attainable while working the problems. Reviewing the general rules presented earlier may help simplify the procedure of verifying an identity.

How To

Given an identity, verify using sum and divergence formulas.

1. Begin with the expression on the side of the equal sign that appears almost circuitous. Rewrite that expression until information technology matches the other side of the equal sign. Occasionally, we might have to modify both sides, but working on simply one side is the most efficient.
2. Look for opportunities to utilize the sum and difference formulas.
3. Rewrite sums or differences of quotients as unmarried quotients.
4. If the procedure becomes cumbersome, rewrite the expression in terms of sines and cosines.

Verifying an Identity Involving Sine

Verify the identity[latex]\,\mathrm{sin}\left(\blastoff +\beta \right)+\mathrm{sin}\left(\alpha -\beta \correct)=two\,\mathrm{sin}\,\blastoff \,\mathrm{cos}\,\beta .[/latex]

Verifying an Identity Involving Tangent

Verify the post-obit identity.

[latex]\frac{\mathrm{sin}\left(\alpha -\beta \right)}{\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta }=\mathrm{tan}\,\alpha -\mathrm{tan}\,\beta [/latex]

Try It

Verify the identity:[latex]\,\mathrm{tan}\left(\pi -\theta \right)=-\mathrm{tan}\,\theta .[/latex]

Using Sum and Difference Formulas to Solve an Application Problem

Permit[latex]\,{Fifty}_{1}\,[/latex]and[latex]\,{L}_{2}\,[/latex]denote two non-vertical intersecting lines, and let[latex]\,\theta \,[/latex]denote the astute bending betwixt[latex]\,{50}_{1}\,[/latex]and[latex]\,{L}_{ii}.\,[/latex]Come across (Effigy). Testify that

[latex]\mathrm{tan}\,\theta =\frac{{one thousand}_{ii}-{m}_{1}}{1+{m}_{one}{1000}_{2}}[/latex]

where[latex]\,{m}_{1}\,[/latex]and[latex]\,{m}_{2}\,[/latex]are the slopes of[latex]\,{L}_{1}\,[/latex]and[latex]\,{L}_{2}\,[/latex]respectively. (Hint: Use the fact that[latex]\,\mathrm{tan}\,{\theta }_{1}={m}_{1}\,[/latex]and[latex]\,\mathrm{tan}\,{\theta }_{2}={one thousand}_{2}.[/latex])

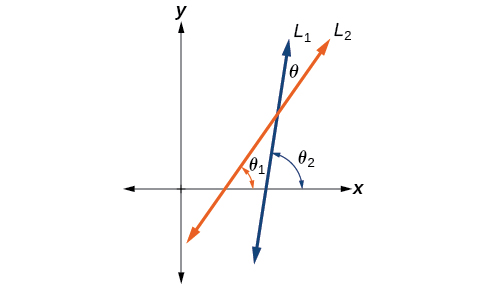
Figure vii.

Investigating a Guy-wire Problem

For a climbing wall, a guy-wire[latex]\,R\,[/latex]is fastened 47 feet high on a vertical pole. Added support is provided by another guy-wire[latex]\,Southward\,[/latex]attached 40 feet in a higher place ground on the aforementioned pole. If the wires are attached to the ground 50 feet from the pole, find the angle[latex]\,\alpha \,[/latex]between the wires. Come across (Figure).

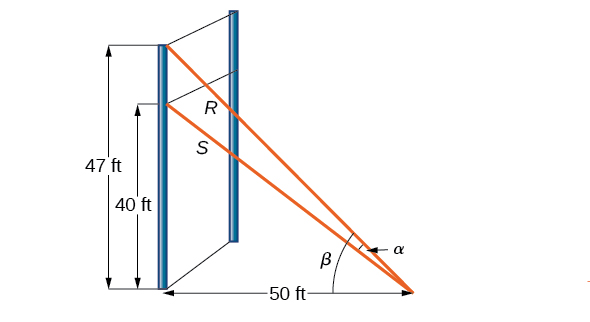
Figure 8.

Analysis

Occasionally, when an application appears that includes a right triangle, we may think that solving is a matter of applying the Pythagorean Theorem. That may be partially true, just information technology depends on what the problem is request and what information is given.

Key Equations

Sum Formula for Cosine	[latex]\mathrm{cos}\left(\alpha +\beta \correct)=\mathrm{cos}\,\blastoff \,\mathrm{cos}\,\beta -\mathrm{sin}\,\alpha \mathrm{sin}\,\beta [/latex]
Difference Formula for Cosine	[latex]\mathrm{cos}\left(\alpha -\beta \correct)=\mathrm{cos}\,\alpha \,\mathrm{cos}\,\beta +\mathrm{sin}\,\alpha \,\mathrm{sin}\,\beta [/latex]
Sum Formula for Sine	[latex]\mathrm{sin}\left(\alpha +\beta \correct)=\mathrm{sin}\,\blastoff \,\mathrm{cos}\,\beta +\mathrm{cos}\,\alpha \,\mathrm{sin}\,\beta [/latex]
Departure Formula for Sine	[latex]\mathrm{sin}\left(\alpha -\beta \right)=\mathrm{sin}\,\alpha \,\mathrm{cos}\,\beta -\mathrm{cos}\,\alpha \,\mathrm{sin}\,\beta [/latex]
Sum Formula for Tangent	[latex]\mathrm{tan}\left(\alpha +\beta \right)=\frac{\mathrm{tan}\,\blastoff +\mathrm{tan}\,\beta }{i-\mathrm{tan}\,\alpha \,\mathrm{tan}\,\beta }[/latex]
Deviation Formula for Tangent	[latex]\mathrm{tan}\left(\alpha -\beta \right)=\frac{\mathrm{tan}\,\alpha -\mathrm{tan}\,\beta }{one+\mathrm{tan}\,\alpha \,\mathrm{tan}\,\beta }[/latex]
Cofunction identities	[latex]\begin{array}{ccc}\hfill \mathrm{sin}\,\theta & =& \mathrm{cos}\left(\frac{\pi }{ii}-\theta \right)\hfill \\ \hfill \mathrm{cos}\,\theta & =& \mathrm{sin}\left(\frac{\pi }{2}-\theta \right)\hfill \\ \hfill \mathrm{tan}\,\theta & =& \mathrm{cot}\left(\frac{\pi }{2}-\theta \right)\hfill \\ \hfill \mathrm{cot}\,\theta & =& \mathrm{tan}\left(\frac{\pi }{2}-\theta \correct)\hfill \\ \hfill \mathrm{sec}\,\theta & =& \mathrm{csc}\left(\frac{\pi }{2}-\theta \correct)\hfill \\ \hfill \mathrm{csc}\,\theta & =& \mathrm{sec}\left(\frac{\pi }{2}-\theta \right)\hfill \terminate{assortment}[/latex]

Key Concepts

• The sum formula for cosines states that the cosine of the sum of two angles equals the production of the cosines of the angles minus the production of the sines of the angles. The divergence formula for cosines states that the cosine of the departure of two angles equals the product of the cosines of the angles plus the product of the sines of the angles.
• The sum and difference formulas can exist used to find the exact values of the sine, cosine, or tangent of an bending. Run into (Effigy) and (Effigy).
• The sum formula for sines states that the sine of the sum of ii angles equals the product of the sine of the first angle and cosine of the second angle plus the product of the cosine of the first angle and the sine of the second bending. The difference formula for sines states that the sine of the difference of ii angles equals the product of the sine of the first angle and cosine of the second angle minus the product of the cosine of the offset angle and the sine of the second bending. Encounter (Effigy).
• The sum and difference formulas for sine and cosine can also be used for inverse trigonometric functions. See (Effigy).
• The sum formula for tangent states that the tangent of the sum of two angles equals the sum of the tangents of the angles divided by 1 minus the production of the tangents of the angles. The difference formula for tangent states that the tangent of the difference of two angles equals the difference of the tangents of the angles divided by ane plus the production of the tangents of the angles. See (Figure).
• The Pythagorean Theorem forth with the sum and deviation formulas can exist used to discover multiple sums and differences of angles. Come across (Figure).
• The cofunction identities apply to complementary angles and pairs of reciprocal functions. Meet (Figure).
• Sum and difference formulas are useful in verifying identities. See (Figure) and (Figure).
• Application problems are oft easier to solve by using sum and difference formulas. See (Effigy) and (Figure).

Department Exercises

Exact

Explicate the ground for the cofunction identities and when they utilise.

Show Solution

The cofunction identities apply to complementary angles. Viewing the two acute angles of a right triangle, if ane of those angles measures[latex]\,x,[/latex]the second angle measures[latex]\,\frac{\pi }{2}-x.\,[/latex]Then[latex]\,\mathrm{sin}x=\mathrm{cos}\left(\frac{\pi }{2}-10\right).\,[/latex]The same holds for the other cofunction identities. The key is that the angles are complementary.

Is in that location just i mode to evaluate[latex]\,\mathrm{cos}\left(\frac{five\pi }{4}\right)?\,[/latex]Explain how to gear up up the solution in two different ways, and so compute to make sure they give the same answer.

Explain to someone who has forgotten the even-odd properties of sinusoidal functions how the addition and subtraction formulas tin determine this feature for[latex]\,f\left(x\correct)=\mathrm{sin}\left(x\right)\,[/latex]and[latex]\,m\left(x\right)=\mathrm{cos}\left(ten\correct).\,[/latex](Hint:[latex]\,0-x=-x[/latex])

Testify Solution

[latex]\mathrm{sin}\left(-x\correct)=-\mathrm{sin}x,[/latex]so[latex]\,\mathrm{sin}x\,[/latex] is odd.[latex]\,\mathrm{cos}\left(-10\right)=\mathrm{cos}\left(0-ten\right)=\mathrm{cos}x,[/latex]so[latex]\,\mathrm{cos}x\,[/latex]is even.

Algebraic

For the following exercises, discover the exact value.

[latex]\mathrm{cos}\left(\frac{7\pi }{12}\correct)[/latex]

[latex]\mathrm{cos}\left(\frac{\pi }{12}\right)[/latex]

Show Solution

[latex]\frac{\sqrt{2}+\sqrt{6}}{4}[/latex]

[latex]\mathrm{sin}\left(\frac{five\pi }{12}\right)[/latex]

[latex]\mathrm{sin}\left(\frac{11\pi }{12}\right)[/latex]

Show Solution

[latex]\frac{\sqrt{6}-\sqrt{two}}{4}[/latex]

[latex]\mathrm{tan}\left(-\frac{\pi }{12}\right)[/latex]

[latex]\mathrm{tan}\left(\frac{19\pi }{12}\right)[/latex]

Bear witness Solution

[latex]-2-\sqrt{3}[/latex]

For the following exercises, rewrite in terms of[latex]\,\mathrm{sin}\,x\,[/latex]and[latex]\,\mathrm{cos}\,ten.[/latex]

[latex]\mathrm{sin}\left(10+\frac{eleven\pi }{6}\correct)[/latex]

[latex]\mathrm{sin}\left(x-\frac{iii\pi }{4}\right)[/latex]

Show Solution

[latex]-\frac{\sqrt{ii}}{2}\mathrm{sin}x-\frac{\sqrt{two}}{2}\mathrm{cos}x[/latex]

[latex]\mathrm{cos}\left(x-\frac{5\pi }{half-dozen}\right)[/latex]

[latex]\mathrm{cos}\left(x+\frac{2\pi }{3}\right)[/latex]

Show Solution

[latex]-\frac{ane}{2}\mathrm{cos}x-\frac{\sqrt{3}}{2}\mathrm{sin}x[/latex]

For the post-obit exercises, simplify the given expression.

[latex]\mathrm{csc}\left(\frac{\pi }{2}-t\right)[/latex]

[latex]\mathrm{sec}\left(\frac{\pi }{2}-\theta \correct)[/latex]

Show Solution

[latex]\mathrm{csc}\theta [/latex]

[latex]\mathrm{cot}\left(\frac{\pi }{ii}-x\correct)[/latex]

[latex]\mathrm{tan}\left(\frac{\pi }{2}-x\right)[/latex]

Show Solution

[latex]\mathrm{cot}ten[/latex]

[latex]\mathrm{sin}\left(2x\right)\,\mathrm{cos}\left(5x\right)-\mathrm{sin}\left(5x\correct)\,\mathrm{cos}\left(2x\right)[/latex]

[latex]\frac{\mathrm{tan}\left(\frac{iii}{ii}10\right)-\mathrm{tan}\left(\frac{7}{5}ten\right)}{1+\mathrm{tan}\left(\frac{iii}{2}x\right)\mathrm{tan}\left(\frac{seven}{five}10\right)}[/latex]

Bear witness Solution

[latex]\mathrm{tan}\left(\frac{x}{10}\right)[/latex]

For the post-obit exercises, discover the requested data.

Given that[latex]\,\mathrm{sin}\,a=\frac{ii}{3}\,[/latex]and[latex]\,\mathrm{cos}\,b=-\frac{1}{four},[/latex]with[latex]\,a\,[/latex]and[latex]\,b\,[/latex]both in the interval[latex]\,\left[\frac{\pi }{2},\pi \right),[/latex]find[latex]\,\mathrm{sin}\left(a+b\right)\,[/latex]and[latex]\,\mathrm{cos}\left(a-b\right).[/latex]

Given that[latex]\,\mathrm{sin}\,a=\frac{4}{five},[/latex]and[latex]\,\mathrm{cos}\,b=\frac{ane}{three},[/latex]with[latex]\,a\,[/latex]and[latex]\,b\,[/latex]both in the interval[latex]\,\left[0,\frac{\pi }{2}\right),[/latex]find[latex]\,\mathrm{sin}\left(a-b\right)\,[/latex]and[latex]\,\mathrm{cos}\left(a+b\right).[/latex]

Show Solution

[latex]\begin{array}{ccccc}\hfill \mathrm{sin}\left(a-b\correct)& =& \left(\frac{4}{5}\right)\left(\frac{1}{3}\right)-\left(\frac{3}{5}\right)\left(\frac{ii\sqrt{2}}{3}\right)\hfill & =& \frac{4-half-dozen\sqrt{ii}}{fifteen}\hfill \\ \hfill \mathrm{cos}\left(a+b\right)& =& \left(\frac{3}{5}\right)\left(\frac{1}{three}\right)-\left(\frac{4}{five}\right)\left(\frac{two\sqrt{2}}{iii}\correct)\hfill & =& \frac{3-8\sqrt{2}}{15}\hfill \end{array}[/latex]

For the following exercises, find the verbal value of each expression.

[latex]\mathrm{sin}\left({\mathrm{cos}}^{-1}\left(0\right)-{\mathrm{cos}}^{-1}\left(\frac{i}{2}\right)\right)[/latex]

[latex]\mathrm{cos}\left({\mathrm{cos}}^{-1}\left(\frac{\sqrt{2}}{2}\right)+{\mathrm{sin}}^{-1}\left(\frac{\sqrt{iii}}{two}\right)\right)[/latex]

Show Solution

[latex]\frac{\sqrt{2}-\sqrt{6}}{4}[/latex]

[latex]\mathrm{tan}\left({\mathrm{sin}}^{-one}\left(\frac{i}{2}\right)-{\mathrm{cos}}^{-1}\left(\frac{one}{2}\right)\correct)[/latex]

Graphical

For the post-obit exercises, simplify the expression, and so graph both expressions as functions to verify the graphs are identical. Confirm your reply using a graphing computer.

[latex]\mathrm{cos}\left(\frac{\pi }{ii}-x\correct)[/latex]

[latex]\mathrm{sin}\left(\pi -10\right)[/latex]

[latex]\mathrm{tan}\left(\frac{\pi }{iii}+10\right)[/latex]

[latex]\mathrm{sin}\left(\frac{\pi }{3}+10\right)[/latex]

[latex]\mathrm{tan}\left(\frac{\pi }{4}-x\correct)[/latex]

[latex]\mathrm{cos}\left(\frac{7\pi }{half dozen}+x\right)[/latex]

[latex]\mathrm{sin}\left(\frac{\pi }{four}+ten\right)[/latex]

[latex]\mathrm{cos}\left(\frac{5\pi }{4}+x\correct)[/latex]

For the following exercises, use a graph to determine whether the functions are the same or different. If they are the same, show why. If they are dissimilar, supplant the second function with one that is identical to the starting time. (Hint: think[latex]\,2x=x+x.[/latex]
)

[latex]f\left(ten\right)=\mathrm{sin}\left(4x\right)-\mathrm{sin}\left(3x\right)\mathrm{cos}\,x,g\left(x\right)=\mathrm{sin}\,x\,\mathrm{cos}\left(3x\right)[/latex]

Show Solution

They are the same.

[latex]f\left(10\right)=\mathrm{cos}\left(4x\right)+\mathrm{sin}\,ten\,\mathrm{sin}\left(3x\correct),g\left(x\right)=-\mathrm{cos}\,x\,\mathrm{cos}\left(3x\right)[/latex]

[latex]f\left(x\right)=\mathrm{sin}\left(3x\correct)\mathrm{cos}\left(6x\right),thou\left(x\right)=-\mathrm{sin}\left(3x\right)\mathrm{cos}\left(6x\right)[/latex]

Show Solution

They are the different, try[latex]\,g\left(ten\right)=\mathrm{sin}\left(9x\correct)-\mathrm{cos}\left(3x\right)\mathrm{sin}\left(6x\right).[/latex]

[latex]f\left(10\right)=\mathrm{sin}\left(4x\right),one thousand\left(ten\right)=\mathrm{sin}\left(5x\right)\mathrm{cos}\,10-\mathrm{cos}\left(5x\right)\mathrm{sin}\,x[/latex]

[latex]f\left(ten\right)=\mathrm{sin}\left(2x\correct),g\left(ten\correct)=two\,\mathrm{sin}\,x\,\mathrm{cos}\,x[/latex]

Show Solution

They are the same.

[latex]f\left(\theta \right)=\mathrm{cos}\left(2\theta \right),g\left(\theta \right)={\mathrm{cos}}^{2}\theta -{\mathrm{sin}}^{2}\theta [/latex]

[latex]f\left(\theta \right)=\mathrm{tan}\left(two\theta \correct),1000\left(\theta \right)=\frac{\mathrm{tan}\,\theta }{1+{\mathrm{tan}}^{2}\theta }[/latex]

Evidence Solution

They are the unlike, attempt[latex]\,g\left(\theta \correct)=\frac{two\,\mathrm{tan}\theta }{1-{\mathrm{tan}}^{2}\theta }.[/latex]

[latex]f\left(x\correct)=\mathrm{sin}\left(3x\right)\mathrm{sin}\,x,thousand\left(ten\right)={\mathrm{sin}}^{2}\left(2x\right){\mathrm{cos}}^{two}x-{\mathrm{cos}}^{2}\left(2x\correct){\mathrm{sin}}^{2}x[/latex]

[latex]f\left(x\right)=\mathrm{tan}\left(-x\correct),grand\left(x\correct)=\frac{\mathrm{tan}\,x-\mathrm{tan}\left(2x\right)}{1-\mathrm{tan}\,x\,\mathrm{tan}\left(2x\right)}[/latex]

Evidence Solution

They are different, try[latex]\,thousand\left(x\right)=\frac{\mathrm{tan}x-\mathrm{tan}\left(2x\right)}{one+\mathrm{tan}ten\mathrm{tan}\left(2x\right)}.[/latex]

Technology

For the following exercises, observe the exact value algebraically, and and so confirm the answer with a reckoner to the 4th decimal point.

[latex]\mathrm{sin}\left(75°\right)[/latex]

[latex]\mathrm{sin}\left(195°\right)[/latex]

Show Solution

[latex]-\frac{\sqrt{three}-1}{2\sqrt{2}},\text{or }-0.2588[/latex]

[latex]\mathrm{cos}\left(165°\right)[/latex]

[latex]\mathrm{cos}\left(345°\correct)[/latex]

Bear witness Solution

[latex]\frac{ane+\sqrt{3}}{2\sqrt{ii}},[/latex]or 0.9659

[latex]\mathrm{tan}\left(-fifteen°\right)[/latex]

Extensions

For the post-obit exercises, prove the identities provided.

[latex]\mathrm{tan}\left(x+\frac{\pi }{iv}\correct)=\frac{\mathrm{tan}\,x+1}{1-\mathrm{tan}\,ten}[/latex]

Prove Solution

[latex]\begin{array}{ccc}\hfill \mathrm{tan}\left(x+\frac{\pi }{4}\right)& =& \\ \hfill \frac{\mathrm{tan}10+\mathrm{tan}\left(\frac{\pi }{4}\correct)}{1-\mathrm{tan}ten\mathrm{tan}\left(\frac{\pi }{4}\correct)}& =& \\ \hfill \frac{\mathrm{tan}x+ane}{1-\mathrm{tan}10\left(1\right)}& =& \frac{\mathrm{tan}x+1}{i-\mathrm{tan}x}\hfill \cease{assortment}[/latex]

[latex]\frac{\mathrm{tan}\left(a+b\correct)}{\mathrm{tan}\left(a-b\right)}=\frac{\mathrm{sin}\,a\,\mathrm{cos}\,a+\mathrm{sin}\,b\,\mathrm{cos}\,b}{\mathrm{sin}\,a\,\mathrm{cos}\,a-\mathrm{sin}\,b\,\mathrm{cos}\,b}[/latex]

[latex]\frac{\mathrm{cos}\left(a+b\correct)}{\mathrm{cos}\,a\,\mathrm{cos}\,b}=1-\mathrm{tan}\,a\,\mathrm{tan}\,b[/latex]

Show Solution

[latex]\begin{array}{ccc}\hfill \frac{\mathrm{cos}\left(a+b\right)}{\mathrm{cos}a\mathrm{cos}b}& =& \\ \hfill \frac{\mathrm{cos}a\mathrm{cos}b}{\mathrm{cos}a\mathrm{cos}b}-\frac{\mathrm{sin}a\mathrm{sin}b}{\mathrm{cos}a\mathrm{cos}b}& =& 1-\mathrm{tan}a\mathrm{tan}b\hfill \finish{array}[/latex]

[latex]\mathrm{cos}\left(10+y\right)\mathrm{cos}\left(x-y\right)={\mathrm{cos}}^{2}10-{\mathrm{sin}}^{two}y[/latex]

[latex]\frac{\mathrm{cos}\left(x+h\right)-\mathrm{cos}\,x}{h}=\mathrm{cos}\,x\frac{\mathrm{cos}\,h-one}{h}-\mathrm{sin}\,x\frac{\mathrm{sin}\,h}{h}[/latex]

Testify Solution

[latex]\begin{array}{ccc}\hfill \frac{\mathrm{cos}\left(x+h\right)-\mathrm{cos}x}{h}& =& \\ \hfill \frac{\mathrm{cos}x\mathrm{cosh}-\mathrm{sin}x\mathrm{sinh}-\mathrm{cos}x}{h}& =& \\ \hfill \frac{\mathrm{cos}x\left(\mathrm{cosh}-ane\right)-\mathrm{sin}x\mathrm{sinh}}{h}& =& \mathrm{cos}x\frac{\mathrm{cos}h-i}{h}-\mathrm{sin}x\frac{\mathrm{sin}h}{h}\hfill \end{assortment}[/latex]

For the following exercises, prove or disprove the statements.

[latex]\mathrm{tan}\left(u+five\right)=\frac{\mathrm{tan}\,u+\mathrm{tan}\,v}{1-\mathrm{tan}\,u\,\mathrm{tan}\,v}[/latex]

[latex]\mathrm{tan}\left(u-v\correct)=\frac{\mathrm{tan}\,u-\mathrm{tan}\,v}{one+\mathrm{tan}\,u\,\mathrm{tan}\,v}[/latex]

[latex]\frac{\mathrm{tan}\left(ten+y\right)}{1+\mathrm{tan}\,x\,\mathrm{tan}\,10}=\frac{\mathrm{tan}\,x+\mathrm{tan}\,y}{one-{\mathrm{tan}}^{2}10\,{\mathrm{tan}}^{2}y}[/latex]

If[latex]\,\alpha ,\beta ,[/latex]and[latex]\,\gamma \,[/latex]are angles in the same triangle, then evidence or disprove[latex]\,\mathrm{sin}\left(\alpha +\beta \right)=\mathrm{sin}\,\gamma .[/latex]

Show Solution

True. Note that[latex]\,\mathrm{sin}\left(\alpha +\beta \correct)=\mathrm{sin}\left(\pi -\gamma \right)\,[/latex]and expand the right hand side.

If[latex]\,\blastoff ,\beta ,[/latex]and[latex]\,y\,[/latex]are angles in the same triangle, then prove or disprove[latex]\,\mathrm{tan}\,\alpha +\mathrm{tan}\,\beta +\mathrm{tan}\,\gamma =\mathrm{tan}\,\alpha \,\mathrm{tan}\,\beta \,\mathrm{tan}\,\gamma [/latex]

Cosine Sum And Difference Identities,

Source: https://courses.lumenlearning.com/suny-osalgebratrig/chapter/sum-and-difference-identities/

Posted by: graingermisiongs.blogspot.com

Share this post